3.1.1. MATERI KULIAH
3.1.1.1. Mambaca Materi Kuliah
Apa itu Mendiskripsikan Data dan Ukuran Pemusatan
Setelah mengumpulkan data, Anda akan memperoleh kumpulan angka-angka. Misalkan setelah mengumpulkan data tinggi dan berat badan mahasiswa, Anda memperoleh kumpulan angka-angka tinggi dan berat badan mahasiswa. Silahkan perhatikan kumpulan angka-angka tinggi dan berat badan sebelum Anda rapikan dan setelah Anda rapikan. Bahkan setelah kumpulan angka-angka tinggi dan berat badan Anda rapikan sekalipun, Anda masih mengalami kesulitan dalam menarik kesimpulan mengenai kumpulan angka-angka tinggi dan berat badan tersebut. Bayangkan bahwa nanti pada saat melakukan penelitian skripsi, Anda akan mengumpulkan data dalam jumlah besar mengenai topik yang Anda teliti. Apa yang perlu Anda lakukan agar dapat mengambil kesimpulan dari data yang telah Anda kumpulkan?
Agar dapat mengambil kesimpulan dari kumpulan angka-angka yang menjadi bagian dari suatu kumpulan data, Anda perlu melakukan perhitungan untuk memperoleh nilai tertentu. Nilai tertentu yang Anda hitung guna mengambil kesimpulan awal mengenai data dikenal dengan istilah umum statistik (statistic). Perhatikan pernyataan yang dikeluarkan oleh institusi yang bertanggung jawab dalam bidang kelautan dan atmosfer Amerika Serikat (National Oceanic and Atmospheric Administration, NOAA) berikut ini: Suhu permukaan bumi telah meningkat sebesar 0,08oC per dasawarsa sejak 1880. Perhatikan pula pernyataan Kepala Dinas Pertanian dan Ketahanan Pangan NTT: Melalui penerapan program tanam jagung panen sapi (TJPS), para petani jagung di NTT mampu memproduksi jagung sebanyak 9 ton/hektar. Apa yang bisa Anda pahami dari kedua pernyataan ini? Apakah di mana-mana di seluruh dunia suhu permukaan bumi naik sebesar 0,08oC setiap 10 tahun? Apakah semua petani yang melaksanakan TJPS memang mampu meningkatkan produksi jagung menjadi 9 ton per hektar? Angka 0,08oC dan 9 ton/hektar dalam kedua pernyataan di atas tampak seakan-akan merupakan statistik. Statistik seharusnya dihitung dari sekumpulan angka. Pada pernyataan pertama, kenanikan suhu sebesar 0,08oC per 10 tahun sangat mungkin dihitung dari sekumpulan data. Namun pada pernyataan kedua, bisa jadi disampaikan karena ada seorang petani yang melaksanakan TJPS mampu memproduksi jagung sampai sebesar 9 ton/hektar. Jadi, silahkan tentukan sendiri, mana dari kedua angka tersebut di atas yang merupakan statistik dan yang bukan merupakan statistik.
Statistik sebagaimana disebutkan di atas kita gunakan untuk membuat kesimpulan awal dari sekumpulan data yang kita miliki. Statistik yang kita hitung dari data untuk membuat kesimpulan awal seperti ini merupakan bagian dari statistika yang dikenal sebagai statistika deskriptif. Keterangan deskriptif dari istilah statistika deskriptif tersebut mengindikasikan bahwa statistik seperti di atas kita gunakan untuk mendeskripsikan data, yaitu untuk menerangkan keadaan data dengan menggunakan ciri-ciri tertentu yang kita hidung dari data. Untuk memahami lebih lanjut apa itu statistika deskriptif, silahkan baca pendahuluan LibreTexts Statistics: Descriptive Statistics, Introduction. Ciri-ciri yang secara umum disebut sebagai statistik tersebut mendeskripsikan data dalam dua hal, yaitu sejauh mana data berpusat pada suatu nilai tertentu dan sejauh mana nilai data menyebar. Ciri yang pertama lazim disebut ukuran pemusatan atau statistik pemusatan, sedangkan ciri yang kedua disebut ukuran penyebaran atau statistik penyebaran. Pada materi kuliah ini kita akan belajar memahami tiga ukuran stau statistik pemusatan, yaitu rata-rata (mean), nilai tengah (median), dan modus (mode), dan mempelajari cara menghitungnya dengan menggunakan fungsi yang tersedia pada program aplikasi Excel.
Macam dan Cara Menenetukan Nilai Ukuran Pemusatan
Sebagaimana telah saya sebutkan di atas, tiga macam statistik digunakan sebagai statistika deskriptif untuk menjelaskan sejauh mana data memusat di sekitar suatu nilai. Ketiga statistik tersebut adalah rata-rata (mean), nilai tengah (median), dan modus (mode). Dari ketiga statistik tersebut, rata-rata dan nilai tengah merupakan ukuran yang berkaitan dengan nilai data, sedangkan modus berkaitan dengan frekuensi nilai suatu data.
Untuk memahami ketiganya, misalkan kita mempunyai kumpulan data yang terdiri atas 11 anggota dengan nilai masing-masing sebagai berikut:
Berdasarkan pada kumpulan data ini:1; 1; 1; 2; 2; 3; 4; 4; 4; 4; 4.
- Rata-rata adalah (1+1+1+2+2+3+4+4+4+4+4)/11; atau ((3*1)+(2*2)+(1*3)*(4*4))/11; atau (3(1)+2(2)+1(*3)+4*(4))/11 =2,7; yang untuk data sampel dilambanhkan dengan huruf x kecil dengan garis di atasnya, dalam bahasa Inggris dibaca x bar dan dalam bahasa Indonesia x rata-rata.
- Nilai tengah (median) yang dilambangkan M adalah nilai yang terletak di tengah jika data diurutkan dari kecil ke besar atau sebaliknya, pada kumpulan data di atas data yang berada di tengah adalah data dengan nilai 3 sehingga median adalah 3 atau M=3.
- Modus (mode) adalah nilai data yang paling banyak terdapat dalam kumpulan data. Dalam kumpulan data di atas, data bernilai 1 terdapat sebanyak 3 kali, data bernilai 2 terdapat sebanyak 2 kali, data bernilai 3 terdapat 1 kali, dan data bernilai 4 terdapat 4 kali sehingga modus dalam kumpulan dara di atas adalah 4 karena terdapat paling banyak.
Dengan contoh sebagaimana yang saya sajikan di atas, mudah-mudahan Anda semua dapat membedakan ketiga statistik pemusatan yang digunakan untuk mendeskripsikan data. Disebut pemusatan karena nilai statistik rata-rata dan nilai tengah menunjukkan nilai yang berada di tengah si dalam kisaran nilai terendah 1 dan nilai tertinggi 4, sedangkan nilai modus menunjukkan nilai data yang paling kerap ditemukan dalam kumpulan data.
Nilai rata-rata atau secara singkat rata-rata yang untuk dilambangkan dengan x rata-rata dengan perhitungan sebagaimana dijelaskan di atas lazim dituliskan dalam bentuk notasi statistika sebagai berikut:
Pada notasi tersebut x dengan garis di sebelah atasnya menyatakan rata-ratadata sampel, X menyatakan data dan i menyatakan urutan data yang mulai dari data pada urutan pertama, yaitu i=1, sampai urutan terbesar, yaitu n. Pada kumpulan data di atas, nilai i adalah 1 dan nilai n adalah 11. Lambang sigma digunakan sebagai penjumlahan berturut-turut, untuk data di atas melambangkan 1+1+1+2+2+3+4+4+4+4+4. Ini adalah pertama kali kita berkenalan dengan lambang dalam belajar statistika, kita akan bertemu dengan lambang semacam ini lebih banyak lagi semkain banyak kita belajar statistika. Rerata yang kita hitung dengan menggunakan rumus seperti ini dikenal semabagi rerata aritmatik (artitmatic mean). Selain rerata artitmatik, juga dikenal rerata harmonik (harmonic mean), rata-rata geometik (geometric mean), dan rata-rata logaritmik (logarithmic mean), silahkan klik tautan masing-masing untuk belajar mengenalinya masing-masing. Satu kumpulan data yang sama mempunyai nilai rata-rata aritmatik, rata-rata harmonik, rata-rata geometrik, dan rata-rata logaritmik yang berbeda, yang masing-masing mempunyai kegunaan yang berbeda pula. Kita tidak akan mendalami lebih lanjut ketiga macam rata-rata tersebut karena dalam bidang pertanian yang paling diperlukan adalah rata-rata aritmatik yang selanjutnya kita sebut rata-rata.
Pada materi 2.1 kita sudah belajar mengorganisasikan data dalam bentuk tabel sebaran frekuensi. Silahkan periksa data kerapatan gulma yang disajikan dalam bentuk tabel sebaran frekuensi tunggak dan sebaran frekuensi kisaran sebagai berikut:
Pertanyaanya kemudian adalah bagaimana cara menghitung rata-rata dari data yang disajikan dalam bentuk tabel sebaran frekuensi tunggal (tabel kiri) dan cara menghitung rata-rata dari data yang disajikan dalam bentuk tabel sebaran frekuensi kisaran (tabel kanan)? Untuk tabel yang disajikan dalam bentuk tabel sebaran frekuensi tunggal, tinggal kita mengganti xi dalam rumus penghitungan rata-rata dengan fi*xi, di mana fi menyatakan nilai frekuensi untuk data ke-i (xi) sehingga nilai x rata-rata kita hitung sebagai (1*1+3*2+5*3 ... +1*13+1*14+1*15)/75. Tapi bagaimana jika yang kita punyai hanya data dalam interval kelas ebagaimana pada tabel di sebelah kanan? Prinsip menghitungnya sama dengan menghitung rata-rata dari data dalam tabel sebaran frekuensi tunggal. Hanya saja, sebelum menggunakan rumus penjumlaham fi*xi, terlebih dahulu kita perlu menghitung nilai titik tengah (midpoint) dari setiap interval kelas. Misalnya titik tengah dari 3-5 adalah (3+5)/2, dari 5-7 adalah (5+7)/2, dan seterusnya. Tapi bagaimana dengan titik tengah dari <=3 dan titik tengah dari >13? Untuk kedua interval kelas ini, kita asumsikan berjarak yang sama dengan interval kelas lainnya, yaitu 2 sehingga karena 3-2=1 dan 13+2=15 maka titik tengah untuk interval kelas <=3 kita hitung sebagai (1+3)/2 dan titik tengah untuk interval kelas >13 kita hitung sebagai (13+15)/2. Dari perhitungan titik tengah interval kelas kita memperoleh nilai titik tengah 2; 4; 6; 8; 10; 12; dan 14 sehingga untuk memperoleh nilai rata-rata, masing-masing kita kalikan dengan nilai frekuensinya, kita jumlahkan hasilnya, lalu kita bagi dengan 75. Silahkan coba lakukan perhitngan sendiri dengan menggunakan Excel.
Setelah memahami pengertian ketiga statistik pemusatan, sekarang mari kita perhatikan kumpulan data berikut yang terdiri atas 14 anggota:
1;11,5;6;7.2;4;8;9;10;6,8;8,3;2;2;10;1
Untuk memudahkan memahami, mari terlebih dahulu kita organisasikan data dengan mengurutkannya dari nilai terkecil menjadi nilai terbesar:
1;1;2;2;4;6;6,8;7.2;8;8,3;9;10;10;11,5
Dari kumpulan data di atas, silahkan hitung nilai rata-rata dan nilai modus. Bisakah Anda memperoleh hasilnya? Memperoleh hasil nilai rata-rata mungkin sangat mudah. Tetapi bagaimana dengan nilai tengah? Karena jumlah data genap, yaitu 14, maka tidak ada data yang terletak di tengah yang nilainya dapat kita gunakan sebagai nilai tengah. Dalam keadaan jumlah data adalah genap maka untuk memperoleh nilai tengah kita jumlahkan dua data yang terletak di tengah setelah data kita urutkan dari nilai terkecil ke nilai tertinggi atau sebaliknya lalu kita bagi dua jumlah nilai kedua data yang terletak di tengah tersebut. Dari data dia atas, dua data yang terletak di tengah adalah data dengan nilai 6,8 dan dengan nilai 7,2 sehingga nilai tengah kumpulan data adalah (6,8+7,2)/2=7. Dalam hal ini nilai tengah data, yaitu 7, bukan merupakan nilai dari salah satu data yang termasuk dalam kumpulan data. Silahkan periksa untuk memastikan. Oleh karena itu, setengah dari kumpulan data yang berjumlah 14 bernilai kurang dari 7 dan setengahnya lagi bernilai lebih dari 7. Silahkan periksa sendiri untuk memastikan.
Setelah membaca uraian di atas, mari kita pelajari cara menggunakan fungsi Excel untuk menghitung nilai rata-rata, nilai tengah, dan nilai moduk suatu kumpulan data. Fungsi dasar Excel untuk menghitung statistik pemusatan rerata, nilai tengah, dan modus adalah berturut-turut AVERAGE, MEDIAN, dan MODE. Cara menggunakan sama dengan cara menggunakan dungsi yang sudah kita pelajari pada materi 2.1, yaitu didahului dengan mengetikan = diiukuti dengan mengetikkan kata fungi yang bersangkutan, lalu memblok data. dan menekan tombol Enter. Silahkan perhatikan penggunaan ketiga fungsi tersebut untuk menghitung statistik dari 9 data di bawah ini:
Selain fungsi dasar, Excel juga menyediakan fungsi bersyarat, antara lain fungsi AVERAGEIF sebagaimana contoh pada tabel di bawah ini:
Pada tabel di sebelah kiri:
- Fungsi =AVERAGEIF(B6:B13,"Toko 1",D6:D13) kita gunakan untuk menghitung nilai rata-rata penjualan semua barang di toko1
- Fungsi =AVERAGEIF(C6:C13,"Barang 2",D6:D13) kita gunakan untuk menghitung nilai rata-rata penjualan barang 2 di kedua toko.
- Fungsi =AVERAGEIF(D6:D13,">10") kita gunakan untuk menghitung rata-rata penjualan bernilai >10 untuk semua barang di kedua toko.
Untuk mencoba melakukan sendiri, silahkan UNDUH file Excel yang berisi data pada tabel kiri. Selain fungsi bersyarat AVERAGEIF, juga tersedia fungsi bersyarat ganda AVERAGEIFS untuk menghitung nilai rata-rata dengan beberapa syarat dan AVERAGEA untuk menghitung nilai rata-rata data angka, karakter, dan logika. dan fungsi MEDIAN IF dan MEDIAN IFS untuk menghitung nilai median bersyarat. Silahkan klik tautan masing-masing untuk mempelajari cara menggunakannya.
Untuk mempelajari lebih lanjut mengenai ketiga statistik ukuran pemusatan dan mengenai fungsi Excel untuk menghitungnya, silahkan baca pendahuluan Ablebits.com: Mean, Median, and Mode in Excel, Contexrures: Excel Average Functions, Excel Median Function Examples, DQLab: Rumus Excel Dasar untuk Analisis Statistik Deskriptif dan Tutorial Analysis ToolPak untuk Teknik Analisis Data Deskriptif, LibreTexts Statistics: Descriptive Statistics, Measures of the Centre of the Data, Statistics by Jim: Descriptive Statistics in Excel (Data Analysis Add-in), Zach Hotzone: Ukuran Pemusatan Data: Mean, Median, Modus
Menggunakan Add-ins Analysis ToolPak dan SmartStatXL untuk Menghitung Statistik Pemusatan
Sebagaimana telah saya sampaikan pada awal kita mulai kuliah statistika, Excel mempunyai Add-in untuk statistika bernama Analysis ToolPak. Add-in ini dapat kita gunakan untuk menghitung statistik pemusatan secara cepat. Selain itu, Analisis ToolPack juga menghitung statistik ukuran penyebaran yang akan kita bahas pada materi kuliah berikutnya serta statistik kemencengan (skewness) dan keruncingan (kurtosis) data yang sudah kita bahas secara sekilas pada materi 2.2. Untuk mempelajari cara menggunakan add-in Analysis ToolPack menghitung statistik pemusatan, statistik penyebaran, dan statistik lainnya, silahkan UNDUH file data tinggi badan dan berat badan mahasiswa.
Proses untuk menentukan statistik pemusatan, statistik penyebaran, dan statistik lainnya dengan menggunakan add-in Analysis ToolPack dikenal sebagai analisis statistik deskriptif atau secara singkat analisis deskriptif.
Langkah-langkah yang Anda lakukan adalah sebagai berikut:
- Siapkan data yang akan Anda analisis dalam tabel. Data dapat terdiri atas beberapa kolom sekaligus, setiap kolom memuat data tertentu, yang dalam statistika dikenal sebagai peubah (variabel, variable). Pada data contoh, data terdiri atas peubah tinggi badan dan berat badan mahasiswa.
- Klik menu Data>Analysis>Data Analysis dan pada kotak dialog yang tampil pilih Descriptive Statistics.
- Pada kotak dialog berikutnya klik Input Range lalu blok data beserta nama peubah masing-masing, klik tombol Column untuk menyatakan bahwa data setiap peubah terdapat pada kolom yang berbeda, klik Labels in first row untuk menyatakan bahwa baris paling atas memuat nama peubah, klik tombol Output Range lalu klik satu sel kosong di sebelah kanan atau di sebelah bawah data sebagai sel yang akan memuat hasil analisis, klik tombol Summary statistics, Confidence Levels for Means, Kth Largest, dan Kth Smallest, lalu klik tombol OK.
Silahkan periksa hasil analisis sebagaimana pada tabel di bawah ini. Baris berwarna di bawah data memuat statistik rata-rata, nilai tengah, dan modus yang dihitung dengan fungsi AVERAGE, MEDIAN, dan MODE serta statistik kemencengan dan keruncingan yang dihitung dengan menggunakan fungsi SKEW dan fungsi KURT. Baris berwarna hijau pada hasil analisis menyajikan statistik rata-rata, nilai tengah, dan modus serta baris berwarna lainnya yang menyajikan statistik kemencengan dan keruncingan hasil analisis dengan menggunakan analisis statistik deskriptif pada pada add-ins Analysis TooolPak. Silahkan bandingkan nilai yang diperoleh dengan menggunakan fungsi dan dengan menggunakan add-in Analysis ToolPak, apakah sama atau berbeda.
Uraian lebih lanjut mengenai penggunaan add-in Analysis ToolPack dalam melakukan analisis deskriptif statistik sebaran akan saya berikan pada materi 3.2. Untuk mendalami penggunaan add-in tersebut dalam melakukan analisis deskriptif, silahkan kunjungi DQLab: Tutorial Analysis ToolPak untuk Teknik Analisis Data Deskriptif dan Statistics by Jim: Descriptive Statistics in Excel.
Untuk menghiitung statistik pemusatan menggunakan add-in SmartStatExcel, silahkan terlebih dahulu unduh dan pasang add-in dari situs SmartStatXL dengan mengikuti panduan yang diberikan. Setelah berhasil memasang add-in maka pada pita menu Excel akan ditambahkan menu tambahan SmartStatXL.
Untuk memulai analyssis, silahkan klik submenu Statistika Deskriptif & Uji Normalitas pada ujung paling kiri pada pita sub-menu SmartSatatXL. Ketika mengklik, akan tampil menu untuk memilih data, silahkan kilim tombol Sumber Data lalu blok data mulai dari judul kolom dan kemudian klik tombol Selanjutnya. Pada menu yang tampil, silahkan pastikan variabel Tinggi Badan (cm) dan berat badan (kg) sudah diklik lalu klik tombol setiap ukuran pemusatan yang diinginkan dan hilangkan tanda centang pada semua tombol Ukuran Penyebaran lalu klik tombol OK. Ad-in StatSmartXL akan membuat sheet baru secara otomatis untuk memuat hasil analisis.
Silahkan buka sheet yang dibuat secara otomatis oleh add-in SmartStatXL dan kemudian periksa hasil analisis, apakah sama dengan hasil dari melakukan analisis dengan menggunakan fungsi Excel dan menggunakan add-in Analysis ToolPak. Untuk memperoleh panduan lebih rinci, silahkan klik panduan yang tersedia pada situs SmartStatXL. Sebagai catatan, add-in SmartStatExcel merupakan add-in dengan fokus untuk melakukan analisis ragam yang akan dipelajari nanti ketika mengambil mata kuliah perancangan percobaan.
Silahkan klik tautan untuk memperoleh data yang saya berikan sebagai contoh pada saat kuliah daring.
3.1.1.2. Mengunduh dan Membaca Pustaka
Materi kuliah yang Anda baca ini hanyalah semacam panduan mengenai bagaimana seharusnya Anda mempelajari materi kuliah ini. Untuk mempelajari materi kuliah ini lebih lanjut, Anda perlu membaca pustaka sebagai berikut:
Pustaka
- Buku Teks: Bowen (2022) Chapter 2 Graph dan Common Distribution Shapes, Schmuller (2016) Part I Chapter 3.
- Website: Ablebits.com: Mean, Median, and Mode in Excel, Contexrures: Excel Average Functions, Excel Median Function Examples, DQLab: Rumus Excel Dasar untuk Analisis Statistik Deskriptif dan Tutorial Analysis ToolPak untuk Teknik Analisis Data Deskriptif, LibreTexts Statistics: Descriptive Statistics, Measures of the Centre of the Data, Statistics by Jim: Descriptive Statistics in Excel (Data Analysis Add-in), Zach Hotzone: Ukuran Pemusatan Data: Mean, Median, Modus
Website
Silahkan mengklik halaman Pustaka Kuliah untuk mengakses dan mengunduh buku teks, mengakses perpustakaan daring dan mengunduh buku teks gratis, mengakses websites, dan mengakses artikel jurnal ilmiah.
1.2.1.3. Kuiz Melaksanakan Kuliah
Setelah membaca materi kuliah dan pustaka kuliah untuk materi kuliah 2.1, materi kuliah 2.2, dan materi kuliah 3.1, setiap mahasiswa wajib mengerjakan kuiz secara mandiri dengan mengklik tautan sebagai berikut:
- Mengerjakan dan Memasukkan Lembar Jawaban Kuiz selambat-lambatnya pada Senin, 3 Oktober 2023 pukul 24.00 WITA
- Memeriksa hasil pemasukan untuk Memastikan Lembar Jawaban Kuiz sudah masuk
Mahasiswa yang tidak mengerjakan quiz tidak akan memperoleh nilai untuk setiap kuiz yang tidak dikerjakan.
3.1.2. TUGAS KULIAH
3.1.2.1. Mendiskusikan dengan Cara Membagikan Materi Kuliah
Setelah membaca materi kuliah, silahkan bagikan materi kuliah melalui media sosial yang dimiliki disertai dengan mencantumkan status tertentu, misalnya "Saya sekarang baru tahu ternyata statistika terapan itu menyenangkan ... dst." Untuk membagikan lauar klik tombol Beranda dan kemudian klik tombol pembagian memalui media sosial dengan mengklik tombol media sosial yang tertera di sebelah kanan judul materi kuliah. Jika media sosial yang dimiliki tidak tersedia dalam ikon yang ditampilkan, klik ikon paling kanan untuk membuka ikon media sosial lainnya. Materi kuliah dibagikan paling lambat pada Senin, 3 Oktober 2023 pukul 24.00 WITA dengan cara menjawab pertanyaan pada laporan melaksanakan kuliah.
3.1.2.2. Mendiskusikan dengan Cara Menyampaikan dan/atau Menanggapi Komentar
Setelah membaca materi kuliah, silahkan buat minimal satu pertanyaan dan atau komentar mengenai materi kuliah. Buat pertanyaan secara langsung tanpa perlu didahului dengan selamat pagi, selamat siang, dsb., sebab belum tentu akan dibaca pada jam sesuai dengan ucapan selamat yang diberikan. Ketik pertanyaan atau komentar secara singkat tetapi jelas, misalnya "Mohon menjelaskan apa manfaat mempelajari statistika terapan". Pertanyaan dan/atau komentar diharapkan ditanggapi oleh mahasiswa lainnya dan setiap mahasiswa wajib menanggapi minimal satu pertanyaan dan/atau komentar yang disampaikan oleh mahasiswa lainnya. Pertanyaan dan/atau komentar maupun tanggapannya disampaikan paling lambat pada Senin, 3 Oktober 2023 pukul 24.00 WITA dengan cara menjawab pertanyaan pada laporan melaksanakan kuliah.
3.1.2.3. Mengerjakan dan Melaporkan Projek Bersama
Untuk menuntaskan pelaksanaan pembelajaran materi 3.1. Pendeskripsian Data 1: Ukuran Pemusatan Data, silahkan kerjakan projek berikut secara berkelompok, maksimum terdiri atas 3 orang mahasiswa:
- Silahkan unduh data padat populasi gulma dimodifikasi dan hitung nilai maksimum dan nilai minimum padat populasi gulma. Ketik nilai maksimum dan nilai minimum yang diperoleh.
- Salin data dari sheet PadatPopulasi dan kemudian tempel pada shee DataRerata, DataMedian, dan DataModus lalu hitung nilai rata-rata padat populasi gulma dengan menggunakan fungsi AVERAGE, nilai tengah padat populasi gulma dengan menggunakan fungsi MEDIAN, dan nilai modus tinggi badan dengan menggunakan fungsi MODE. Unggah file setelah dilakukan perhitungan dan bagian namamahasiswa dalam nama file diganti dengan nama masing-masing.
- Salin data dari sheet PadatPopulasi dan kemudian tempel pada sheet baru dengan nama AnalysisToolpack lalu hitung nilai rata-rata, median, dan modus padat populasi gulma dengan menggunakan add-in Analysis ToolPack. Unggah kembali fike yang sama, tetapi setelah memuat hasil analisis dengan menggunakan add-in Analysis ToolPak dan bagian namamahasiswa dalam nama file diganti dengan nama masing-masingg.
- Salin data dari sheet PadatPopulasi dan kemudian tempel pada sheet baru dengan nama SmartStatXL lalu hitung nilai rata-rata, median, dan modus padat populasi gulma dengan menggunakan add-in SmartStatXL. Unggah kembali file file yang sama, tetapi setelah memuat sheet baru yang memuat hasil analisis dengan menggunakan add-in SmartStatXL dan bagian namamahasiswa dalam nama file diganti dengan nama masing-masing.
- Dari mengerjakan analisis ukuran pemusatan data yang telah Anda lakukan pada butir 2 sampai butir 3, apakah nilai rerata, nilai tengah, dan modus yang diperoleh adalah sama dan tentukan langkah mana yang akan Anda gunakan nanti pada saat menganalisis data hasil penelitian skripsi.
Silahkan memasukkan laporan pengerjaan projek bersama tersebut di atas dengan cara menjawab pertanyaan yang sesuai pada formulir Laporan Melaksanakan Kuliah paling lambar pada Senin, 3 Oktober 2023 pukul 24.00 WITA.
3.1.3. ADMINISTRASI PELAKSANAAN KULIAH
- Menandatangani Daftar Hadir Melaksanakan Kuliah selambat-lambatnya pada Rabu, 27 September 2023 pukul 24.00 WITA dan setelah menandatangani, silahkan periksa untuk memastikan daftar hadir sudah ditandatangani;
- Menyampaikan Laporan Projek Kuliah dan Mengerjakan Tugas selambat-lambatnya pada Senin, 3 Oktober 2023 pukul 24.00 WITA dan setelah memasukkan, silahkan periksa untuk memastikan laporan sudah masuk.
Mahasiswa yang tidak mengisi dan menandatangani Daftar Hadir Melaksanakan Kuliah dan tidak menyampaikan Laporan Melaksanakan Kuliah akan ditetapkan sebagai tidak melaksanakan kuliah.
***********
Hak cipta blog pada: I Wayan Mudita
Diterbitkan pertama kali pada 3 September 2022, belum pernah diperbarui.
Diterbitkan pertama kali pada 3 September 2022, belum pernah diperbarui.
Hak cipta selurun tulisan pada blog ini dilindungi berdasarkan Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. Silahkan mengutip tulisan dengan merujuk sesuai dengan ketentuan perujukan akademik.


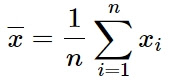







Apakah Penggunaan Fitur Data Analysis sesewaktu dapat memberikan hasil yang kurang cermat?
BalasHapusDan apakah versi Aplikasi dab versi windows mempengaruhi kinerja Data Analysis ini?
Penggunaan fitur Data Analysis dalam aplikasi tertentu dapat memberikan hasil yang kurang cermat tergantung pada sejumlah faktor, termasuk kualitas data yang dimasukkan, metode analisis yang digunakan, dan pemahaman pengguna terhadap statistik. Ketika melakukan analisis data, sangat penting untuk memahami asumsi yang mendasari algoritma yang digunakan dan memeriksa apakah data memenuhi asumsi tersebut. Juga, perlu mempertimbangkan apakah data perlu diolah lebih lanjut sebelum analisis.
HapusApakah ada kekurangan saat menggunakan data analytics untuk menghitung suatu data statistik dibandingkan dengan menggunakan fungsi excel biasa? Jelaskan!
BalasHapusData Analytics dapat diartikan sebagai serangkaian aplikasi mulai dari Basic Intelligence,reporting and online Anlytical Processing dan beberapa fitur lainnya. Data analystic ini sangat membantu untuk mendapatkan kesimpulan dari informasi data dibandingkan fungsi excel biasa. Data Analytics mempermudah perhitngan statistik, menjadikan waktu perhitungan semakin efisien, hasil perhitngan yang akurat dan reliable. Kekurangan dari data analytics ini adalah membutuhkan tools khusus untuk memperosesnya.
HapusMengapa rata rata disebut sebagai ukuran kecendrungan sentral? Lalu apa saja bilangan yang sering digunakan dalam ukuran tendensi sentral?
BalasHapusKarena :
HapusRata-rata hitung (mean), median dan modus disebut dengan ukuran kecenderungan terpusat (measure of central tendency). Sebab kecenderungan dari nilai-nilai tersebut memusat pada bagian tengah suatu perangkat data. Serta,
Terdapat tiga ukuran tendensi sentral yang sering digunakan yaitu: Mean, yaitu rata-rata hitung atau rata-rata aritmatika. Median, yaitu nilai tengah. Modus, yaitu nilai yang sering muncul.
Komentar ini telah dihapus oleh pengarang.
BalasHapusMengapa Mean, Median dan Modus tersebut dinamakan ukuran pemusatan data?
BalasHapuskarena ukuran pemusatan data merupakan salah satu pengukuran data dalam statiska yang terdiri dari modus(nilai yang sering muncul), median(nilai tengah), mean(penghitung rata ratag
HapusKarena ukuran pemusatan data termasuk pengukuran data dalam statistika terdiri atas (Mean,Median,Modus). Adanya ketiga poin tersebut pada data yang sedang kita dianalisis menegaskan bahwa (Mean,Median, Modus) merupakan ukuran dari pemusatan data.
HapusKomentar ini telah dihapus oleh pengarang.
BalasHapusKomentar ini telah dihapus oleh pengarang.
HapusHal apa saja yang membedakan antara deskriptif statistik untuk setiap individual dan analisis deskriptif untuk kombinasi variabel.
BalasHapusStatistik deskriptif hanya terbatas pada menyajikan data bentuk tabel, diagram, grafik, dan besaran lain. Sedangkan statistik inferensial selain mencakup statistik deskriptif juga mampu dipakai untuk melakukan estimasi dan penarikan kesimpulan terhadap populasi dari sampelnya.
HapusMengapa Mean dikatakan sebagai indikator statistik dalam mengukur rata-rata dari sebuah data yang tersedia?
BalasHapusMean dikatakan sebagai indikator stastitik karena Dalam kasus umum, nilai mean dapat diartikan sebagai satu angka yang mewakili keseluruhan dataset. Nilai rata-rata tersebut didapatkan dari hasil penjumlahan seluruh nilai yang ada dari masing-masing data, kemudian dibagi dengan banyaknya data yang ada.
HapusMengapa rumus AVERAGE, MEDAN, MODE sering sekali muncul dalam kumpulan data, Apa yang mempengaruhi dari 3 rumus diatas sering muncul dalam pengumpulan data?
BalasHapusMean, median, dan modus sangat diperlukan dalam menganalisis suatu hasil atau pengumpulan data. Misalkan pada kasus nilai ulangan matematika. Penerapan mean (rata-rata) dapat ditunjukkan saat menentukan berapa banyak siswa yang mendapatkan nilai di atas rata-rata nilai kelas.
HapusMedian digunakan apabila guru ingin membagi kelas menjadi dua kelompok berdasarkan urutan nilai.
Modus dapat digunakan oleh guru untuk mengetahui berapa banyak siswa yang memperoleh nilai tertentu atau menentukan frekuensi terbanyak dari suatu data.
Disaat seperti digunakan pengolahan data dengan memperhitungkan nilai Median dan Mean dalam kehidupan sehari hari
BalasHapusApakah ada cara lain yang bisa digunakan untuk mengukur pemusatan data pada statistik selain mean,median,dan modus?
BalasHapusIya ada yaitu
Hapusrata-rata geometrik dan Rata-rata Harmonik (H).
1. Rata-rata geometrik adalah akar ke-n dari hasil perkalian unsur-unsur datanya. Rata-rata geometrik sering digunakan dalam bisnis dan ekonomi untuk menghitung rata-rata tingkat perubahan, rata-rata tingkat pertumbuhan, atau rasio rata-rata untuk data berurutan tetap atau hampir tetap atau untuk rata-rata kenaikan dalam bentuk persentase.
2. Rata-rata Harmonik (H) adalah kebalikan dari nilai rata-rata hitung (aritmetik mean). rata-rata harmonik sering digunakan sebagai ukuran tendensi sentral untuk kumpulan data yang menunjukkan adanya laju perubahan, seperti kecepatan.
Komentar ini telah dihapus oleh pengarang.
HapusJelaskan, Bagaimana cara menentukan nilai ukuran pemusatan dengan menggunakan data analysis ? Serta Bagaimana cara menganalisis ukuran pemusatan data tunggal dan data kelompok?
BalasHapusMengapa mean dapat dipengaruhi oleh outlier (data ekstrem)?
BalasHapus